Let
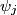 be the eigenfunctions of the operator be the eigenfunctions of the operator 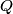 . Let . Let 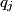 be the eigenvalue associated with be the eigenvalue associated with 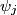 . Expand . Expand 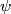 in terms of the eigenstates in terms of the eigenstates 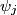 of of 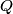 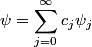 Then 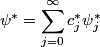 So, 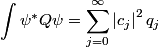 which is the expectation value of the physical observable that 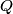 represents. Therefore, answer (C) is correct. represents. Therefore, answer (C) is correct. |